
動機
シミュレーションの作成
実地調査
結果
補足・今後の展望
注釈・参考資料
1.動機
皆さんもご存じの通り、いつも昼頃になると広大の食堂には行列ができています。私もよく食べに行きますが、食堂を利用する目安になればよいと考え、「人の流れはどのようになっているのか」、「いつ頃から行列ができはじめるのか」、「並んだときどれくらい待てばよいのか 」ということを調査しました。
2.シミュレーションの作成

| V1 | 食堂への流入速度(人/min) |
| V2 | 配膳所への流入速度(人/min) |
| V3 | レジの速度(人/min) |
| V4 | 食堂からの流出速度(人/min) |
| S1 | 食堂への流入速度(人/min) |
| S2 | 食堂への流入速度(人/min) |
| S3 | 食堂への流入速度(人/min) |
表1.[変数の説明]
食堂の人の流れを観察し、以下のような「貯水槽モデル」を考案しました。 V1を時系列に沿った入力(一分あたりの人数=人/min)としV2~V4,S1~S3は以下のように再帰的に定義されます。
| S2M | 配膳所の最大収容人数(人) |
| VR | レジの最大速度(人/min) |
| ET | 食事の所要時間(一定)(min) |
| S(t)=S1(t-1)+S2(t-1)+V1(t) V3を定義 if(s(t) <= VR) V3(t)=S(t) else V3(t)=VR end if SS(t)=S(t)-V3(t) S1,S2,V2を定義 if(SS(t) <= S2M) S2(t)=SS(t) V2(t)=V1(t) else S2(t)=S2M V2(t)=V3(t) end if S1(t)=SS(t)-S2(t) V4,S3を定義 V4(t)=V3(t-ET) S3(t)=S3(t-1)+V3(t)-V4(t) (tは経過時間) |
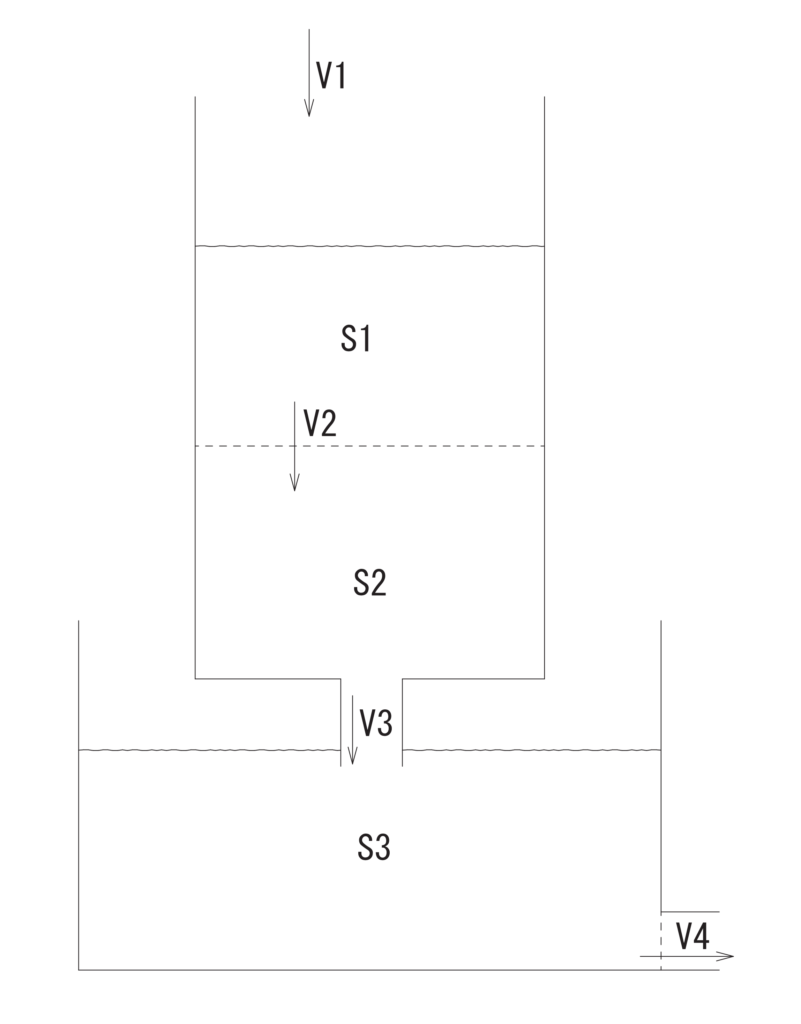
上の表現は分かりにくいので図で視覚的にとらえられるようにしました。
※画像をクリックで拡大(新ページで開きます)
図2.貯水槽モデルの説明 上の水槽にV1で水が入っていき、上の水槽から下の水槽へV3で水が移動し、下の水槽からV4で流れ出る。また上の水槽の点線を水がV2で通過している。上の水槽の点線より上にある水の量がS1、下がS2、下の水槽がS3となる。
3.実地調査
シミュレーションを考えるに当たり実際に西2食堂で行列の人数調査と各種の値の計測を行いました。
3.A.人数調査
2015年5/8,5/13,5/15,5/20,7/1,11/02の約11:40~12:20の間の西2食堂の行列について1分ごとに並ぶ人数を調査しました。調査には自作の1分カウンター(※1)を使いました。これがシミュレーションのV1(入力データ)になります。
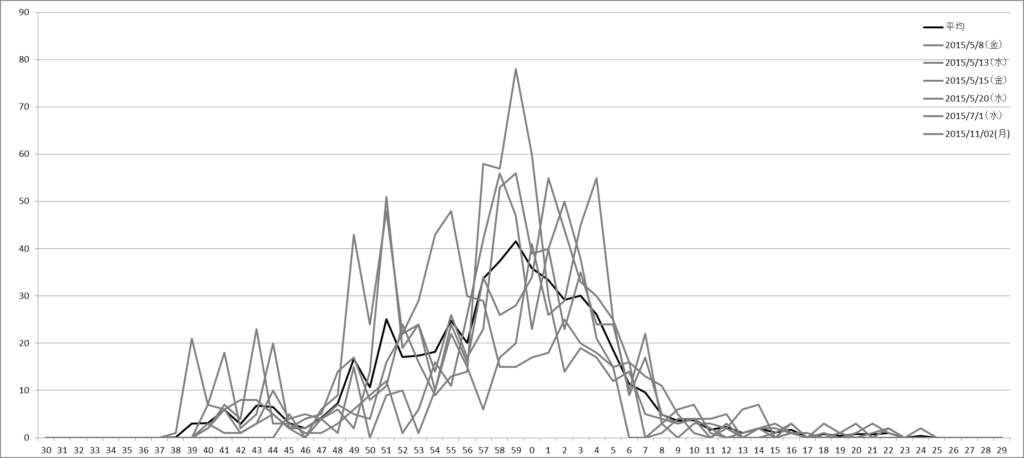
図を見ると11:50頃から人が来はじめ12:00頃に最大となり12:10頃にはもう並ぶ人が居なくなっていることがわかります。
また11/02にはGPSで行列の最後尾の座標も計測しました。
3.B.値の計測
シミュレーションで使う値を計測しました。
| 定数名 | 値 | 注釈 | |
|---|---|---|---|
| 配膳所の最大収容人数(人) | S2M | 102 | ※2 |
| レジの速度(人/min) | VR | 14 | ※3 |
| 食事の所要時間(一定)(min) | ET | 26 | ※4 |
| 行列の密度(m/人) | d | 0.5 | ※5 |
| ホールの座席数 | 453 | ※6 | |
| ホールの混雑度数 | 0.825607064 | ※7 |
表3.[各値の説明]
4.結果
4.A.シミュレーションの結果
5/8,5/13,5/15,5/20,7/1の人数調査の結果 について2コマ目の授業数(教養教育+総合科学部開講授業)による重み付き平均をとりV1としました。 調査範囲外の時間については1人/minとしました。
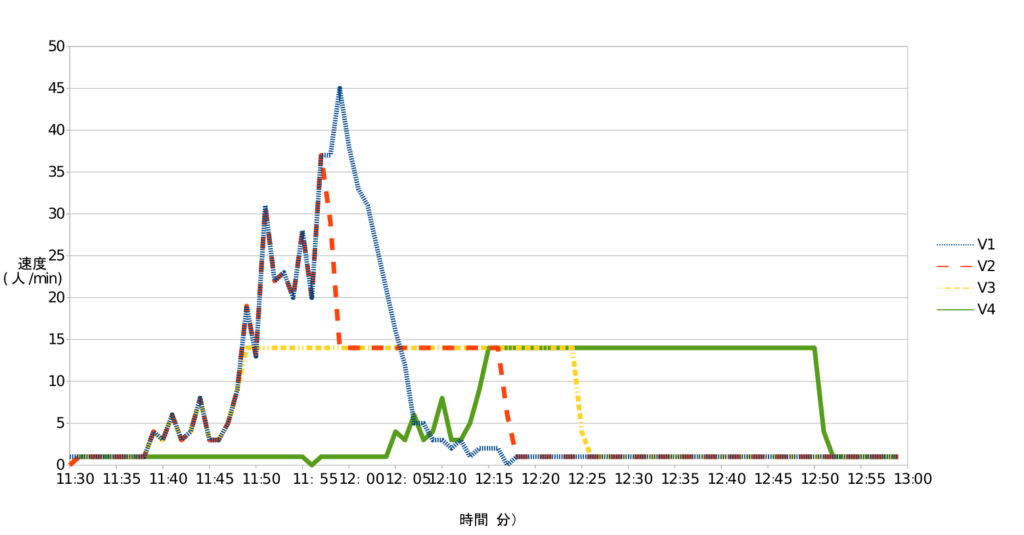
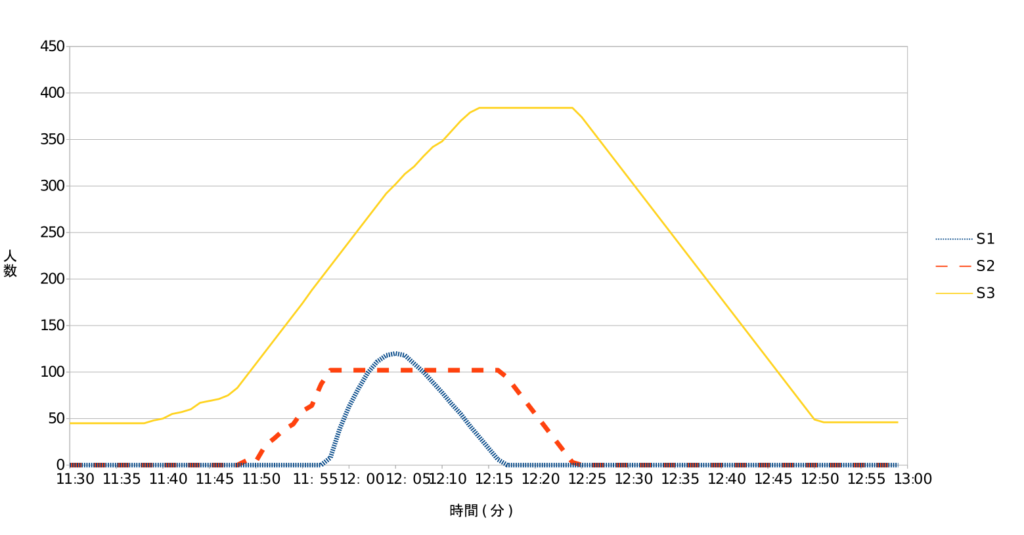
図からV2がVRに達したときからS2が増加し始め、S2がS2Mに達したときからS1が増え始める(=行列が出来始める)ことがわかります。このシミュレーションの結果では11:58~12:16の間に行列が出来ています。
またS3について最大値は384人(12:14~12:24)ですがこの時の混雑度数は0.848となり(※8)測定した値に近いといえます。
4.B.行列の長さの比較
V1とGPSの座標データは11/02のものを使用しました。
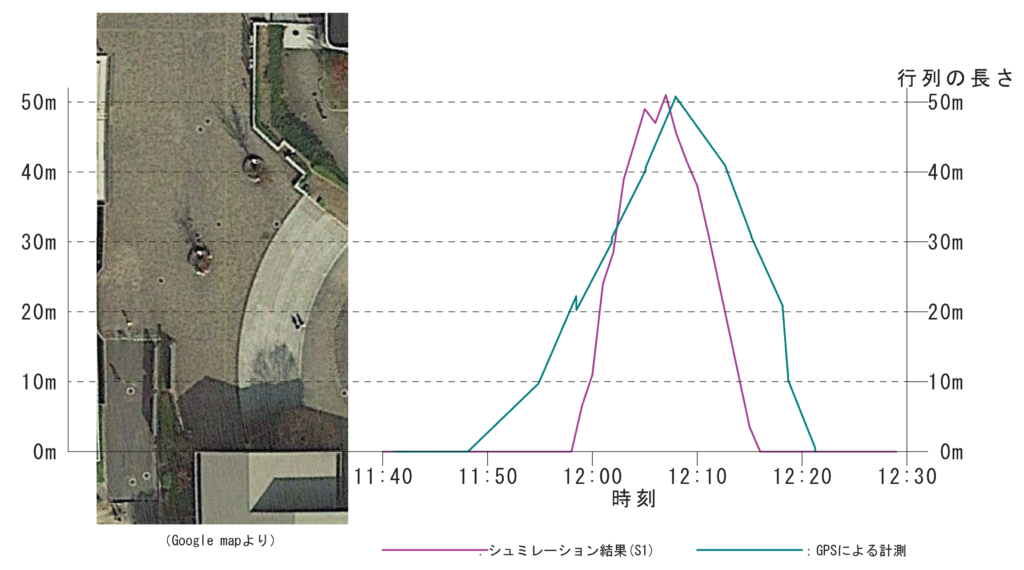
行列の長さLはL=[人数]×d(密度)で与えられます。よってシミュレーションの結果のS1から行列の長さを計算することが出来ます。また実際の長さは行列の最後尾の座標と西2食堂の入り口の座標の差を取ることで計算することが出来ます。
行列の長さについては最大値がシミュレーションの結果が51m(12:07)、GPSによる計測が50.79m(1 2:07.55)となりかなり正確に予測することが出来ました。
補足の項にも書いてありますが、この場合はある程度正確に予測することが出来たと考えられますがこれは偶然に近いものでどの場合も正確かどうかは不明です。
4.C.行列の長さと待ち時間
4.Aと同じデータを使いました。
待ち時間(WT)について、今回のシミュレーションではWT=[行列に並んでいる時間]+[配膳所にいる時間]=S1/V2+S2/V3となります。上記の結果より行列が出来ている状況ではS2=S2M,V2=V3=VRとなっているので、S1=L×dとするとWT(min)はL(m)を用いて以下のように表せます。
WT=(S1+S2M)/VR=(L/d+S2M)/VR
数値を代入するとWT=7.2857+L/7となります。
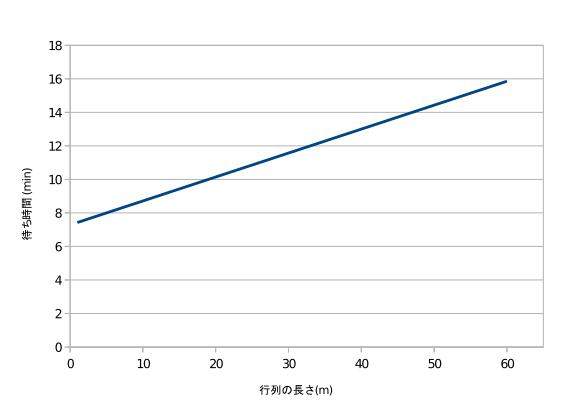
またそこから 並ぶ時間と食べ始める時間の関係を計算することができます。
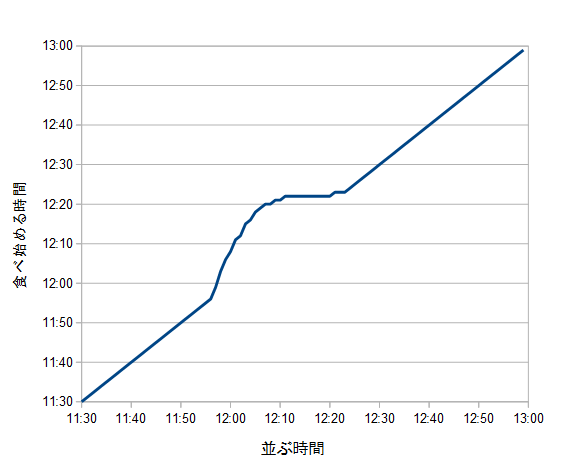
上記の結果から並ぶ人(V1)はいないが行列(S1)がある状態(約12:10~12:20)のとき行列が長いとき並んでも行列が無くなってから並んでも食べ始める時間はあまり変わらないことがわかります。つまり行列が減り始めたらいつ並んでも食べ始める時間は変わらないということです。
5.補足・今後の展望
この調査では5/8,5/13,5/15,5/20,7/1,11/02の6回についてデータをとりましたがその数は多いとはいえません。また一人でしたためV1しか取れずシミュレーションの評価が困難になってしまいました。さらに行列の長さを測定するためにGPSを使いましたが、自分の機器では平均誤差が約3mありあまり信頼できるデータではありません。よって今後の展望としてはデータの充実を図ることとシミュレーションの評価方法を考案することを考えています。
※上記の内容は自由に使っていただいていいですが万一の場合の責任は取れません。
6.注釈・参考資料
※以下の中で太字の数字は仮定したものであり実際に測ったものではない
※以下の中で太字の数字は仮定したものであり実際に測ったものではない
※1 自作の1分カウンター
(http://pn675.html.xdomain.jp/self-work/1mcounter.html)
※2 配膳所について以下のようになった
| タイルの数 | 950.25 | 枚 | |
| タイル一枚当たりの面積 | 0.09 | m^2 | 30cm四方 |
| 面積 | 82.5225 | m^2 | |
| 人間の専有面積 | 0.25 | m^2 | 50cm四方 |
| 荷物+お盆の係数 | 2 | 倍 | |
| 利用係数(密度) | 0.6 | 倍 | |
| 最大収容人数 | 102 | 人 |
[最大収容人数]=[面積]×[利用係数]/( [人間の専有面積]×[荷物+お盆の係数] )(小数点以下切捨て)と計算できる
※3 2015/05/21の12:07~12:17の間のV3の平均
※4 「日常の食事」に関するアンケート調査レポート(食の未来研究所) http://shoku-mirai.com/rd.html?p=19&q19=y より昼食にかける時間の男女別棒グラフから平均時間を算出
※5 2015/05/28の12:15頃のS1より計測
約15mで30人並んでいた よってd=15/30=0.5
※6 西2食堂ホールの見取り図より
※7 2015/05/21の12:23に計測
空席が79席だったので[ホールの混雑度数]=(453-79)/453=0.825607064
※8 384/453=0.848…となる

